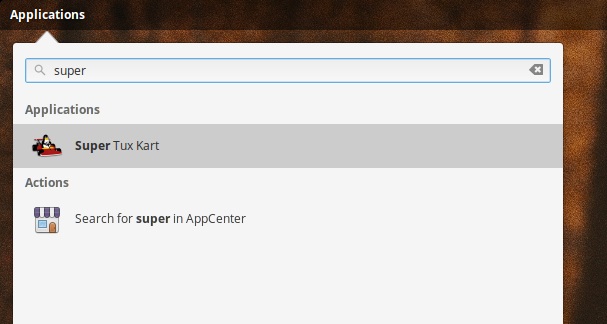
Linux桌面创建启动器
简介
在 Linux 中,一个 .desktop
文件就是一个用来运行程序的快捷方式。没有 .desktop
的话,你的应用就不会在应用菜单中显示了,也无法使用像 Synapse 和 Albert
这样的第三方启动起启动了。
大多数应用在安装后都会自动创建 .desktop
文件,并将自己放入应用菜单中以方便访问。然而,如果是你自己从源代码中编译的程序或者自己下载的压缩格式的应用,那就不会做这些事情了,每次你都需要打开终端来执行它的二进制文件。显然这个过程很无聊也很麻烦。
本文将会告诉你如何为应用创建 .desktop
文件,从而让你能在应用菜单中启动该应用。
创建启动器
.desktop
文件基本上就是一个包含程序信息的纯文本文件,通常根据是自己可见还是所有用户可见的不同而放在
~/.local/share/applications 或者
/usr/share/applications/
目录中。你在文件管理器中访问这两个目录,都会看到很多系统中已安装应用对应的
.desktop 文件存在。
为了演示,我将会为 Super Tux Kart 创建一个 .desktop
文件,这是一个我很喜欢玩的卡丁车竞赛游戏。Ubuntu
仓库中带了这个游戏,但版本一般不新。
要获得最新的版本就需要下载 tar 包,解压并执行其中的游戏启动文件。
你可以仿照这个步骤来为任何程序创建启动器。
注意:下面步骤假设程序压缩包放在 “Downloads” 目录下。
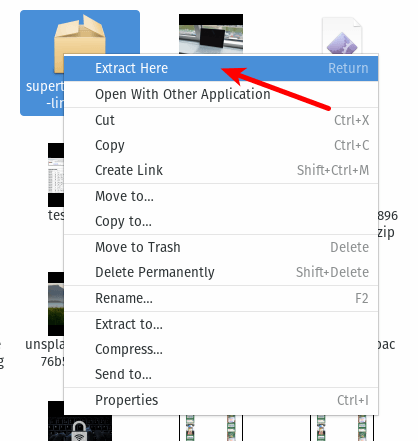
- 跳转到存放压缩包的目录,右击然后选择 “Extract here”。
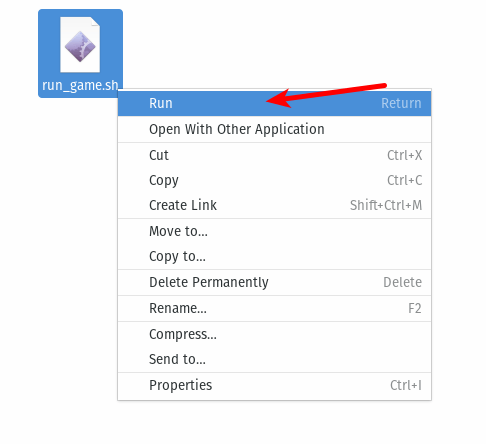
- 解压后,进入新创建的目录然后找到可执行的文件。之后右击文件选择 “Run” 来启动程序,确定程序运行正常。
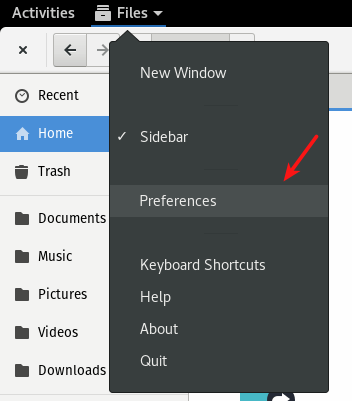
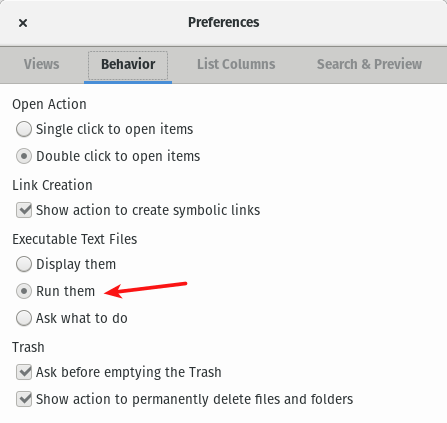
- 有时候,你在右键菜单中找不到 “Run” 选项。这通常是因为这个可执行文件是一个文本文件。你可以在终端中执行它,如果你使用 GNOME 的话,可以点击上面菜单栏中的 Files 菜单,然后选择 “Preferences”。
- 选择 “Behavior” 标签页然后选择 “Executable Text Files” 下的 “Run them”。现在右击可执行文本文件后也能出现 “Run” 选项了。
- 确认应用运行正常后,就可以退出它了。然后运行你的文本编辑器并将下面内容粘贴到空文本文件中:
1
2
3
4
5
6
7
8[Desktop Entry]
Encoding=UTF-8
Version=1.0
Type=Application
Terminal=false
Exec=/path/to/executable
Name=Name of Application
Icon=/path/to/icon
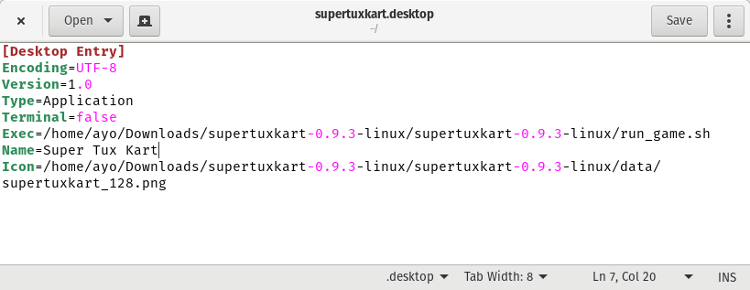
你需要更改 “Exec” 域的值为可执行文件的路径,并且将 “Name” 域的值改成应用的名称。大多数的程序都在压缩包中提供了一个图标,不要忘记把它也填上哦。在我们这个例子中,Super Tux Kart 的启动文件看起来是这样的:
- 将文件以
application-name.desktop为名保存到~/.local/share/applications目录中。.local目录位于你的家目录下,是一个隐藏目录,你需要启用 “Show Hidden Files” 模式才能看到它。如果你希望这个应用所有人都能访问,则在终端中运行下面命令:1
sudo mv ~/.local/share/applications/<application-name`.desktop`> /usr/share/applications/
当然,别忘了把命令中的 <application-name.desktop>
改成真实的 .desktop 文件名。
- 完成后,打开应用菜单,就能看到应用出现在其中,可以使用了。
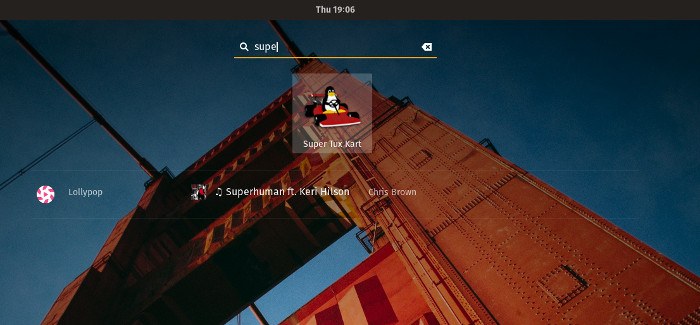
这个方法应该适用于所有主流的 Linux 操作系统。下面是另一张 Super Tux Kart 在 elementary OS 的应用启动器 (slingshot) 上的截图